2014 Statistical Risk Assessment

Our project's statistical risk assessments provide one answer to that question. At the start of this year, we tinkered with the models used to generate those assessments and applied the new machinery to the inputs that were available at the time, much of it still from 2012 (see this post). By early May, all of our sources had updated their data through year-end 2013 or later, allowing us, in turn, to update our risk assessments. In future years, we expect to post updates like these to our website in the spring, as soon as all of the requisite data become available. This year, though, while that website is still under construction, we're making do with a later release via this interim blog.

Now, without further ado: The dot plot below shows the 30 countries identified by our statistical analysis as being at greatest risk this year of new episodes of state-led mass killing. Following best practices in fields like meteorology and election forecasting, we use an ensemble approach to assess risks of these episodes, combining forecasts from a few different models instead of trying to identify the single best one. The gray dots mark the forecasts from the three models in our current ensemble, and the red dots mark their average, which we regard as our single best forecast. The scale of those forecasts is the estimated probability of onset, which you can read as a percent chance (e.g., 0.10 equals 10 percent). For more information on what we mean by an "onset of state-led mass killing" and what the statistical analysis entails, see the Technical Details section at the end of this post.

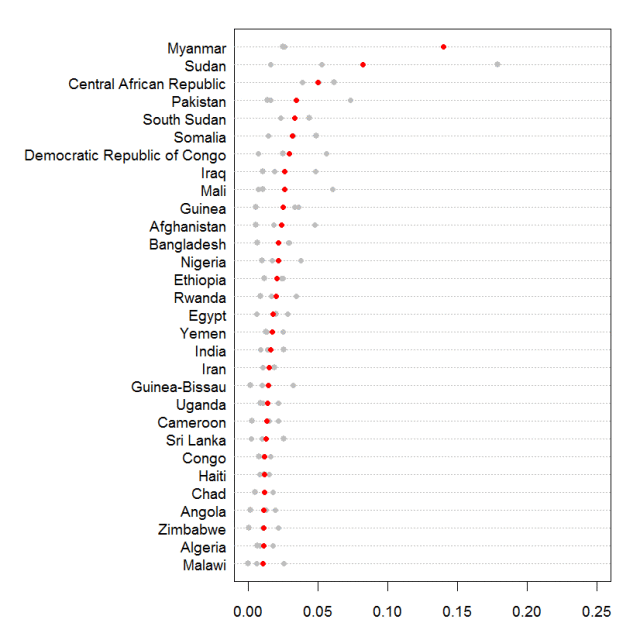
30 Countries at Greatest Risk of a New Episode of State-Led Mass Killing

We call out the top 30 because we are confident that nearly all new episodes of state-led mass killing will occur in countries our models put in that tier.

Exactly which of those countries will see these episodes is much harder to say. Onsets of state-led mass killing occur very rarely; since World War II, the average number of onsets worldwide each year is less than two. With events that rare and relevant data hard to come by, the statistical models we can build to assess risks of these events are inevitably imprecise. At this point, statistical analysis can do a good job distinguishing the highest-risk cases from the rest of the world, but it cannot pinpoint where and when onsets of state-led mass killing will occur. To try to tease out differences in this higher-risk set, to track changes in that risk over time, and to identify vulnerable cases our models might have overlooked, we turn instead to our opinion pool, a "wisdom of crowds" system that elicits and combines similar forecasts from a collection of subject-matter experts.

One way to check the reliability this process is to look back at the statistical risk assessments we produced last year with data from 2012 and see how they fared. As noted at the top, the models have changed a bit, but the basic process is identical.

• In 2013, we saw onsets of state-led mass killing in at least two countries: Egypt (against the Muslim Brotherhood and other anti-coup activists; see here and here), and Nigeria (against alleged supporters of Boko Haram; see here). Both of those countries were in our top 30 at the time—Egypt at 6th and Nigeria at 21.
• We also saw new mass-killing episodes begin last year in Central African Republic—first against alleged supporters of anti-balaka militias that resisted Séléka rebels who overthrew the government in March, and then against Muslims loosely presumed to support Séléka. Here, both the role of the now-collapsed state and the timing of the onsets of the mass-killing episodes were more ambiguous. In any case, CAR was also in our top 30 at the time, at 27th.
• The civil war that started in South Sudan in December 2013 has also produced twin streams of mass killing—one perpetrated by state security forces and their allies against Nuer and others presumed to support the rebels, and another perpetrated by those rebels, mostly targeting Dinka (see here). It's difficult to pinpoint when those episodes of mass killing began, but South Sudan was near the very top of our risk list in 2013 and remains there in 2014.

We can also visualize our updated statistical assessments using a heat map.

Here is the global risk landscape that emerges from the latest available data. Each step up on the color scale corresponds roughly to a doubling of estimated risk—from less than 1 to 1–2 percent, from 1–2 to 2–4 percent, and so on.

---

Estimated Risk of New Episodes of State-Led Mass Killing

If you compare that picture and the dot plot to the ones we drew with data from 2012 (here), you'll see that not much has changed. Most of the factors included in our models are structural features of countries' politics, economy, and society that hold steady in most cases from year to year. So, most of the countries that made their way toward the top of the global list before remain there now, and most of the rest of the world remains at very low risk.

Most, but not all. In the update, three countries saw fairly substantial changes in their estimated risk of new episodes of state-led mass killing.

• Syria dropped out of the global top 30 because of a change in the form of its national political regime, which became even more authoritarian, according to Polity. It might seem counter-intuitive, but the most dictatorial regimes are actually somewhat less susceptible to coup attempts and new civil wars, and thus to onsets of state-led mass killing, than more liberal authoritarian regimes are. And to be clear: this is an assessment of the risk that another episode of state-led mass killing will begin in Syria, in addition to the one that is already occurring. Our models are trained to assess the risk that a new episode of state-led mass killing will occur in a given country at some point during the calendar year. So, by design, our statistical risk assessments say nothing about whether or not ongoing episodes of state-led mass killing will continue, intensify, or cease.
• Ecuador also dropped out of the top 30 because of a decline in the polarization of its national politics, according to Polity. Democracies with factionalism, as Polity calls it, are exceptionally vulnerable to the forms of political instability that nearly always precede and precipitate state-led mass killing, so this shift in Ecuador is a welcome development.
• Iran jumped into the global top 30 because its forecast from our machine-learning algorithm got worse. That algorithm doesn't lend itself to tidy interpretations of the causes of changes in its output, so we can't say exactly why Iran's estimated risk has increased. What we can say is that our statistical process now identifies it as one of the highest-risk countries in the world, because Iran now has a configuration of risk factors that look more like ones in state-led mass killings from the past.

As always, the vast majority of countries continue to have estimated risks that are quite small and statistically indistinguishable from one another. Onsets of state-led mass killing are very rare events, and our statistical estimates reflect that fact. In the set of countries with estimated probabilities of onset under 1 percent, small changes in estimated risk can produce what look like big changes in rank ordering. These changes in rank order should not be interpreted as meaningful changes in risk.

---

Technical Details

We consider a state-led mass killing to have occurred if the deliberate actions of state agents or other groups acting at their behest result in the deaths of at least 1,000 noncombatant civilians over a period of one year or less.

• State-led refers to cases in which the relevant violence is carried out by uniformed troops, police, or other agents of state security, or by other groups acting at the behest of government officials. In cases where the state’s role is ambiguous, we look for evidence of government encouragement of violence or coordination with state policies or military operations.
• A noncombatant civilian is any person who is not a current member of a formal or irregular military organization and who does not apparently pose an immediate threat to the life, physical safety, or property of other people.
• The reference to deliberate actions distinguishes mass killing from deaths caused by natural disasters, infectious diseases, the accidental killing of civilians during war, or the unanticipated consequences of other government policies. Fatalities should be considered intentional if they result from actions designed to compel or coerce civilian populations to change their behavior against their will, as long as the perpetrators could have reasonably expected that these actions would result in widespread death among the affected populations. Note that this definition also covers deaths caused by other state actions, if, in our judgment, perpetrators enacted policies/actions designed to coerce civilian population and could have expected that these policies/actions would lead to large numbers of civilian fatalities. Examples of such actions include, but are not limited to: mass starvation or disease-related deaths resulting from the intentional confiscation, destruction, or medicines or other healthcare supplies; and deaths occurring during forced relocation or forced labor.
• To distinguish mass killing from large numbers of unrelated civilian fatalities, the victims of mass killing must appear to be perceived by the perpetrators as belonging to a discrete group. That group may be defined communally (e.g., ethnic or religious), politically (e.g., partisan or ideological), socio-economically (e.g., class or professional), or geographically (e.g., residents of specific villages or regions). In this way, apparently unrelated executions by police or other state agents would not qualify as mass killing, but capital punishment directed against members of a specific political or communal group would.

Countries can experience more than one episode of state-led mass killing at the same time, if and when the state targets more than one discrete group in distinct conflicts. Sudan is a contemporary example, with ongoing episodes of state-led mass killing in Darfur and South Kordofan. Consequently, all states are theoretically at risk of a mass-killing onset every year, even if they already have one or more episodes of mass killing ongoing. Because all states are theoretically at risk of an onset all the time, all country-years are included in the statistical analysis.

Of course, rebel groups and other non-state actors also kill civilians, and sometimes on a scale that also meets our definition of mass killing. Our statistical risk assessments only consider state-led mass killing, however, because they are produced by models that have to be “trained” on historical data, and at present we only have deep and reliable data on mass killings carried out by states. If and when we are able to produce or obtain comparable data on mass killings perpetrated by non-state groups, we will expand our statistical modeling to incorporate them as well.

Our statistical risk assessments are an average of forecasts from three models representing some different ideas about the origins of mass atrocities or how to assess them.

All of these models are developed from and applied to publicly available data from reputable sources.

• Drawing on work by Barbara Harff and the Political Instability Task Force, the first model emphasizes features of countries' national politics that hint at a predilection to commit genocide or "politicide," especially in the context of political instability. Key risk factors in Harff's model include authoritarian rule, the political salience of elite ethnicity, evidence of an exclusionary elite ideology, and international isolation as measured by trade openness.
• The second model takes a more instrumental view of mass killing. It uses statistical forecasts of future coup attempts and new civil wars as proxy measures of things that could either spur incumbent rulers to lash out against threats to their power or usher in an insecure new regime that might do the same.
• The third model is really not a model but a machine-learning process called Random Forests applied to the risk factors identified by the other two. The resulting algorithm is an amalgamation of theory and induction that takes experts’ beliefs about the origins of mass killing as its jumping-off point but also leaves more room for inductive discovery of contingent effects.

All of these models are estimated from historical data that compares cases where state-led mass killings occurred to ones where they didn't. In essence, we look to the past to identify patterns that will help us spot cases at high risk of mass killing now and in the future.

To get our single-best risk assessment, we simply average the forecasts from these three models. We prefer the average to a single model's output because we know from work in many fields—including meteorology and elections forecasting—that this "ensemble" approach generally produces more accurate assessments than we could expect to get from any one model alone. By combining forecasts, we learn from all three perspectives while hedging against the biases of any one of them.

Researchers interested in replicating and extending our latest analysis can find the data and code they need to do that through this Github repository.